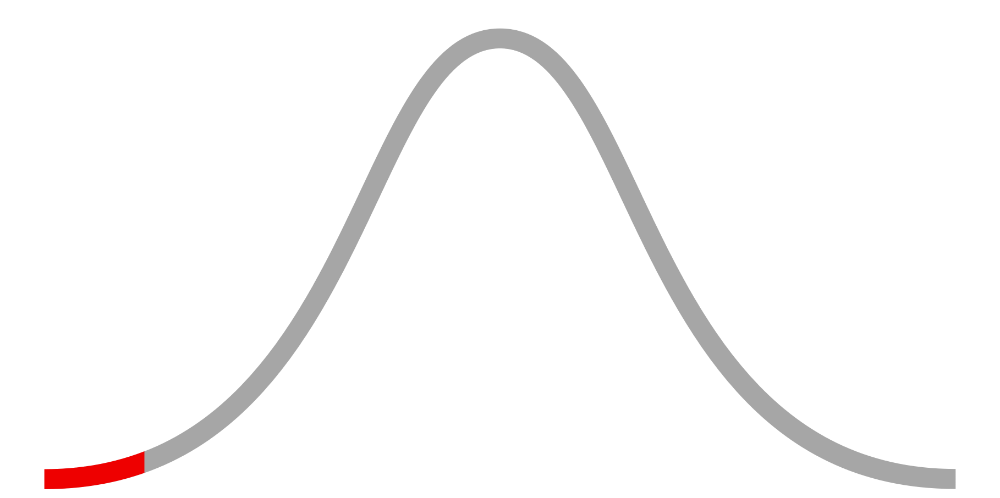
In Taylor Swift's hit 2014 album called "1989," the single track called "Shake it Off" gained worldwide attention for its catchy beat and dismissal of negativity surrounding Swift's public image. Indeed, the lyrics repeat phrases like "the haters gonna hate, hate, hate, hate, hate." Compared to Swift's other songs, "Shake it Off" is unique because there is limited mention of personal romance, drama, and feelings. Rather, the song uses words and phrases related to Swift's intended actions, not her emotional state. Taylor Swift's slight use of language related to positive and negative affect demonstrate an above average example of the Emotion attribute.

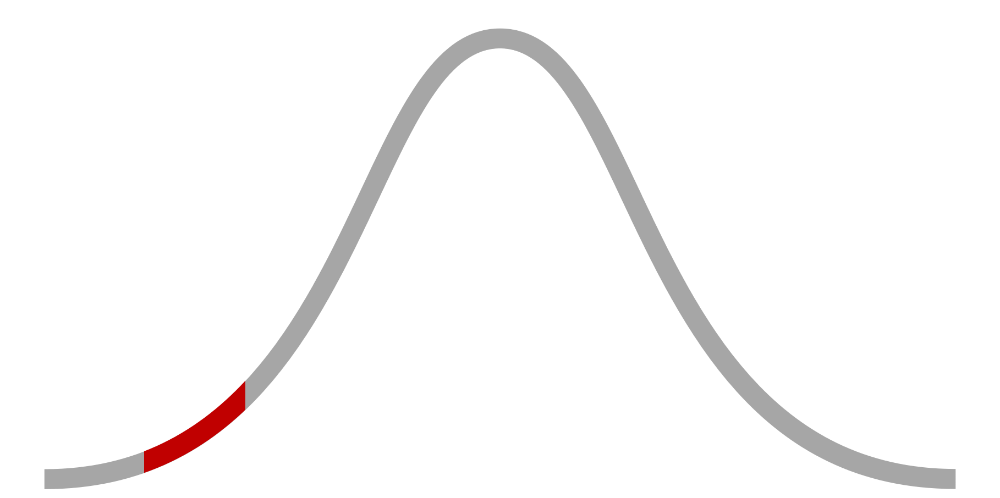
In the hit movie The Fast and the Furious: Tokyo Drift (2006), outlaw teenager Sean Boswell finds himself in Japan after getting kicked out of America by the law and his own mother. After befriending a car enthusiast at school, he's in an underground car enthusiast meetup focused on a style of racing called drifting. As he's walking around, Sean spots a girl from his class and begins flirting with her while discussing technical aspects of car engines. Soon, though, the girl's boyfriend notices and walks over to join the conversation. Sean doesn't realize that the man is part of the crime family known as the Yakuza, and continues taunting him. Despite warnings from two people, Sean decides to race DK ("Drift King") after being allowed to borrow another character's car. Sean bombs the race, wrecks the car, and eats his words because of his inexperience with the drift style of racing. Sean's inability to self-monitor his aggression and impulses in a dangerous, novel setting demonstrates a total lack of the Apperception attribute.

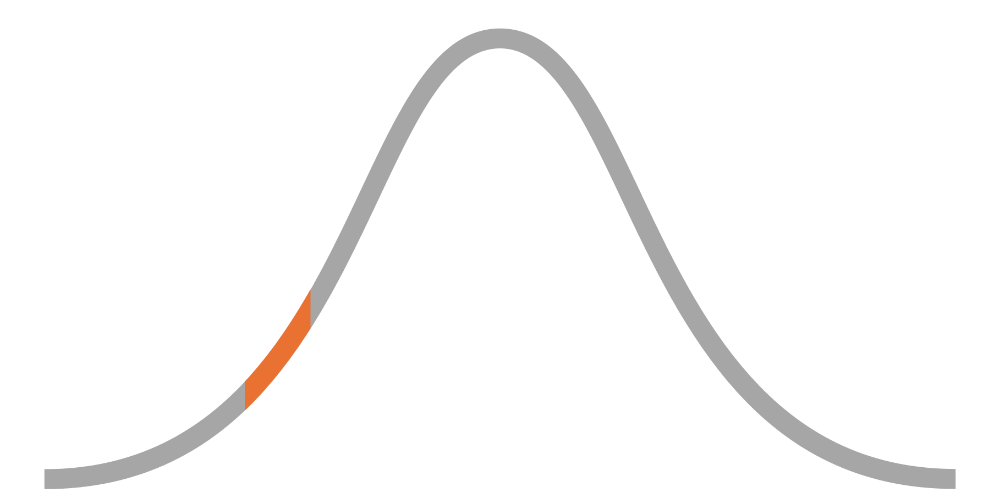
When Ukrainian president Volodymyr Zelenskyy met U.S. President Donald J. Trump, the visitor made the mistake of telling President Trump how Americans were going "to feel" in the future. This caused a problem as the discussion unfolded.

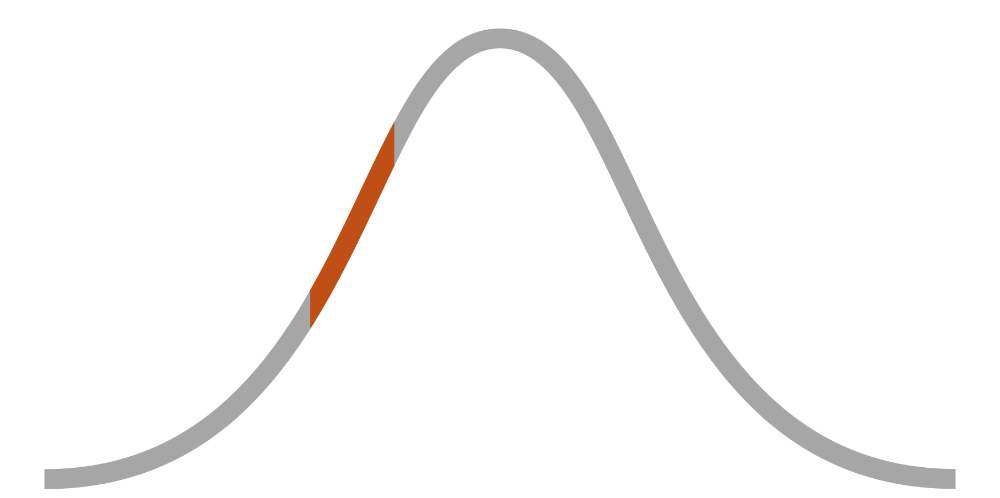
In 2017, the popular Spanish song "Despacito" by Luis Fonsi and Daddy Yankee was remixed with the inclusion of Justin Bieber. The new "Despacito - Remix" version includes Bieber singing in both English and Spanish. During the English portion, the lyrics recount longing and passion for a romantic partner. Lyrics like "My sunrise on the darkest day / Got me feelin' some kind of way" and "The way you nibble on my ear, the only words I wanna hear" reference visual, physical, and auditory sensory perception, and demonstrate a typical example of the Sensation attribute.